Простая, на первый взгляд, задача
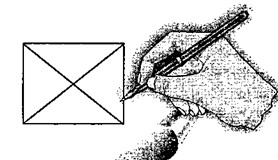
Сопоставление четных и нечетных величин может помочь при решении не только химических задач. Рассмотрим одну из них, ее иногда вспоминают при заполнении досуга. Необходимо нарисовать показанный прямоугольник с двумя диагоналями, не отрывая карандаша от бумаги и не проводя по одной линии дважды.
Первое, с чего начинает каждый новичок — пытается нарисовать эту фигуру, соблюдая поставленные условия. После нескольких попыток он убеждается, что задача неразрешима, и лишь затем возникает желание ее проанализировать, хотя заранее можно было предположить, что именно с этого следовало начать.
Точки, где сходятся прямые, назовем узлами. В показанной фигуре имеется два типа узлов. Один узел находится в центре прямоугольника, в нем сходятся четыре прямых, назовем его четным узлом. В вершинах прямоугольника находятся четыре узла, в которых сходятся по три прямых, это нечетные узлы. Свойства четных и нечетных узлов различны. Четные узлы для решения задач такого типа очень «удобны», в такие узлы можно свободно входить и выходить в процессе рисования, и никаких сложностей с ними не возникает. Отличительное свойство таких узлов состоит в следующем: сколько раз вы из этого узла вышли, столько же раз должны войти (иначе вы его превратите в нечетный). Следовательно, такие узлы не составят никаких проблем, если они будут встречаться на середине пути.
Совсем иные свойства у нечетных узлов, количество входов и выходов не совпадает. Следовательно, на промежуточном этапе такие узлы должны быть исключены. Далее, если вы начали рисование с нечетного узла, то возвращаться в него можно, но затем обязательно следует выйти, завершить на нем рисунок нельзя, иначе узел превратиться в четный. Точно такие же рассуждения приводят нас к выводу, что нечетный узел может быть в конце пути (если начинать рисунок не с него). Окончательный итог — рисование надо начинать с одного нечетного узла и заканчивать на другом, в середине пути не должно быть нечетных узлов.
Посмотрим внимательно на исходный рисунок, в нем четыре нечетных узла, а допустимо, как мы установили, только два, следовательно, задача неразрешима.
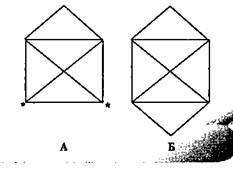
Показанную неразрешимую задачу легко превратить в решаемую, если добавить еще две линии, превратив предыдущий рисунок в конверт (вариант А). В итоге нечетных узлов стало два. Следует только помнить, что необходимо начинать с одного из нечетных узлов и заканчивать на втором (обозначены звездочками).
Задача еще более упрощается, если все узлы четные (вариант Б). Рисовать можно, начиная с любого узла, и в итоге, как показали предыдущие рассуждения, вы неизбежно вернетесь в исходную точку.
Рассуждения справедливы по отношению к узлам, в которых сходится любое количество линий, главное только четность или нечетность узла.
Отзывов (20) на «Простая, на первый взгляд, задача»
Ваш отзыв
Вы должны войти, чтобы оставлять комментарии.
17 Ноя 2011 в 10:51
Спасибо за интересную информацию, попробовал нарисовать фигуру, пока не получилось, буду тренироваться.
17 Ноя 2011 в 11:01
Василий у Вас очень интересный сайт, хотелось бы быть в друзьях вашего сайта.
17 Ноя 2011 в 11:22
Очень интересная задачка. Получилось нарисовать с 3-го раза ))
17 Ноя 2011 в 11:40
Я на такой задачке попадалась)))) Термоэлектричество говорите,а я тоже химик по специальности — моя специализация-физическая химия — корррозия. Давайте дружить сайтами!!!!
17 Ноя 2011 в 14:15
Интересная задача. С первого раза и не получается нарисовать
17 Ноя 2011 в 14:31
В детстве часто такие задачки решали, мне нравилось домик рисовать
17 Ноя 2011 в 14:41
На первый взгляд вроде все просто, но после анализа действительно не все так ладно, как кажется
17 Ноя 2011 в 17:23
С головоломкой этой беда-всю голову сломал.
17 Ноя 2011 в 17:25
Спасибо, прикольно.
17 Ноя 2011 в 17:57
Помню, в детстве часто рисовали открытые конверты не отрывая руки!
17 Ноя 2011 в 18:39
Я голову ломать жалко, а тренировать полезно.
17 Ноя 2011 в 18:42
Решение этой задачки я знаю давно.
Но все равно интересно было освежить в памяти.
Сегодня задам этот ребус младшему сыну.
Пусть думает, развивает логику и заодно — пусть учится не сдаваться и доводить все до конца — в жизни это качество очень пригодится.
Спасибо за статью.
17 Ноя 2011 в 19:21
Интересная задачка.С первого раза не получилось нарисовать.
17 Ноя 2011 в 19:24
На первый взгляд вроде все просто, но после анализа действительно не все так просто )))
17 Ноя 2011 в 19:52
такие задачки очень развивают логически ум.
Ох и злю всегда когда не получается, зато когда сделаешь чувствуешь зарядку ума реально!!!
17 Ноя 2011 в 20:02
Неплохая «зарядка для ума». Спасибо.
17 Ноя 2011 в 20:14
Благодарю Вас за статью! Желаю успехов во всём!
17 Ноя 2011 в 21:04
Логические игры, и различной сложности головоломки, весьма хорошо тренируют ум и сообразительность.
17 Ноя 2011 в 21:45
да интересно, помню 1 раз мне попалась такая задача на упаковки какой-то ерунды(что-то вроде чипсов)
17 Ноя 2011 в 23:21
Как всегда интересно и оригинально! Спасибо!